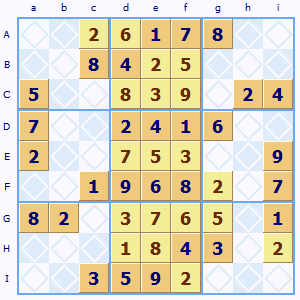
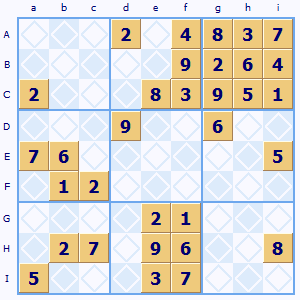
Sudoku X Wing strategy for solving hard puzzles

Yes, I agree you haven't overlooked anything too easy.

I can't see anything forced by the only choice; only square; subgroup exclusion or twin exclusion sudoku strategies.

Always useful at this stage to look through the possibilities one by one using the possibility bar.

In this case it is the '5's that are helpful. In row F there are only two options Fb or Fh. If it was Fb then that has knock on effects, in row H the 5 would have to be in Hc but in area Da the only square left would be Dc. So putting 5 in Fb would require a 5 in the same column c for Dc and Hc. This can not be right - the 5 must go in Fh - no other choice.

If you do that sudoku assignment the rest follows fairly easily I think.

Any comments ? Click here to contribute

Hello,

You said, about the puzzle "Another challenge": "In this case it is the '5's that are helpful. In row F there are only two options Fb or Fh. If it was Fb then that has knock on effects, in row H the 5 would have to be in Hc but in area Da the only square left would be Dc. So putting 5 in Fb would require a 5 in the same column c for Dc and Hc. This can not be right - the 5 must go in Fh - no other choice."

When you talk about the two options for the 5s in F, I see you. When you say 5 in Fb, the 5 in the H row is Hc, I see that. But when you bring up the Da box(area), and say that "the only square left would be Dc", I don't follow you.

I assumed you are saying that the only square left for a 5 is Dc, but didn't you already a 5 in the Da box/area? Why talk about a second 5 in the Da box? The 5 has already been placed slot Fb at the beginning for the Da box/area.

Obviously if you were to place a second 5 in that box, it would have to in Dc and would be in conflict with the 5 in Hc. But that is two 5s in the same box Fb and Dc!?!

I did a check on that option, it is works, out, but I obviously don't understand the logic.

Could I get some help?

CBK

Any comments ? Click here to contribute

Sorry, yes I was wrong, not sure what I was thinking.

I still think the correct strategy was to choose between Fb and Fh for where to place a 5.

If you choose Fb you can prove this is incorrect - but by a longer chain than I thought - however all the steps are straightforward 'forced' choices (only place or only square).

First look at column c. 9 must go in Dc; 4 in Gc; 6 in Ec; 7 in Cc and 5 in Hc to complete the column.

Now complete row C with 6 in Cb and 1 in Cg.

Now go to column g with 9 in Bg and 4 in Eg and 7 in Ig.

It now gets to the crunch in column b. 1 must go in Ib but this forces an impossible allocation of 3 - it must go in BOTH Bb abd Db. This means the initial Fb choice was wrong - it must be the other alternative.

There's probably a better way of proving this but I can't see one.

Apologies again.

Any comments ? Click here to contribute

Here is a puzzle that has an X-Wing in it.

Click to download this puzzle

Any comments ? Click here to contribute

I believe there is one further Swordfish in the example Swordfish puzzle on the strategy page but not the one you suggest.

The rules is that you need three rows and columns with only a pair of particular possibilities in them.

So row A has 2 '9's but row F has 4 '9's and row G has 3 '9's . Columns b and f have 2 but g has 3 '9's . So they do not form a Swordfish.

There is another Swordfish there though with row A; row E and Row I all having just a pair of '9's and they interconnect via columns c; f and g. Using these you can discount the possibility in Gf and Fg. These are some of the same squares discounted by the example Swordfish shown on the strategy page. This often happens, there is more than one way to skin cat!

Any comments ? Click here to contribute

Re. Alexander's comment on the swordfish definition: either the rule Alexander offers is wrong or else the example on the x-wing/dragon page is wrong. The example of the swordfish with 9's has four 9's in row F and three 9's in row G. The example, however, does have only two nines in each of its columns, and this is fundamental to the removal of the extra 9's in rows F and G. But, if we accept the definition that fits the example, namely exactly two 9's in EITHER rows OR columns, we return to the paradox I originally mentioned, namely that there is another swordfish that results in different removals. Something fishy here!

Any comments ? Click here to contribute

I've included a picture of the Swordfish puzzle to make it clear what I meant.

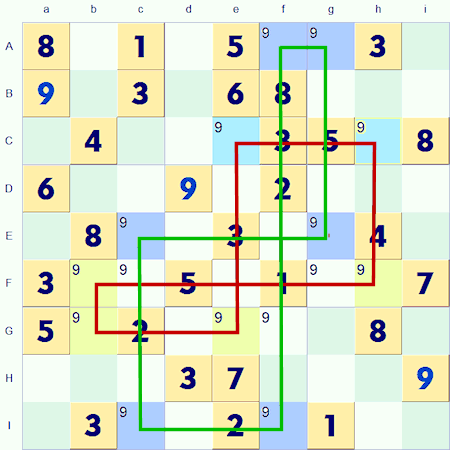
The rows that have pairs of '9's have been highlighted in blue: Row A; C; E and I.

The columns that have pairs of '9's have been highlighted in yellow/green columns b; e and h

As Ce and Ch are in both rows and columns I've colored them bright greeny blue.

That means there is a swordfish through columns b;e and h (as these columns all have only pairs of possibilities) shown as a red line

This is the example swordfish on the strategy page.

The Red swordfish knocks out the possibilities in Fc; Fg and Gf as they are in the same rows as corner points of the red swordfish.

The second swordfish that I indentified in my response is in green colored line.

It is in rows A;E and I (as these rows all have only pairs of possibilities)

The Green swordfish knocks out possibilities in squares Fc; Fg and Gf (the same squares) as they are in the same columns as corner points of this green swordfish.

Any comments ? Click here to contribute

Thanks, Alexander, for an excellent write-up. The key to my understanding is that the swordfish corners are unique in rows OR columns, which was my thought, but was not clear from the Strategy page.

I would nominate your description as a replacement for the Strategy page-- it is much clearer than the present content.

Any comments ? Click here to contribute

The square Gi looks like it can take 1; 4 or 6.

Sudokudragon is just showing squares where a 6s might possibly go, and not showing the other numbers.

Yes Gf must take a 6, but for other reasons than Swordfish and Alternate Pairs, it must be a 6 because of the shared sub-group rule in Row H. So may be a better example should have been chosen. It shows that you can use different rules to achieve the same end result. Gi can not take a 6, both because of Alternate Pairs and also because of Shared Sub-groups.

Any comments ? Click here to contribute