Alternate coloring of pairs is Sudoku solving strategy
Cycles and Twins X-Wing and Swordfish What makes a 'Difficult' puzzle Stripes Word puzzle query Trial and Error - The Labyrinth C Shape Is Sudoku a game of Mathematical symmetry? Is placing the correct candidates part of logic? Two out of three lines This web site has now, at last, extended its repertoire of descriptions of strategies to the more advanced Hook (X-Y Wing) and Alternate Pairs (Conjugate pairs). There is also a step-by-step guide of these advanced
techniques here.
As alternate pairs also lets you spot X-Wing and Swordfish it can be a very useful technique.
Do you use these advanced techniques and how useful in practice are they? Please contribute your thoughts here.
Any comments ? Click here to contributeAn icy waste
Any comments ? Click here to contributeA few years ago I would have said yes, give it a go.
Nowadays I think Sudoku has passed its peak of popularity and the market is rather cluttered with books and web sites.
Also I think the joy of Sudoku is using several strategies not just one, you then are constantly faced with the choice of which one to use. Most of the strategies on SudokuDragon could be thought of as 'shortcuts' for simple cases rather than using a more complex.
Good luck.
Any comments ? Click here to contributeHi, I'm trying to understand how the alternate square coloring excludes the numbers which I show as excluded according to the Possiblities info. I see a few alternate '67' squares but can't seem to extend it to exclude the squares indicated. Can someone please explain the steps that lead to these exclusions? Thanks.
Any comments ? Click here to contributeYes the alternate pair strategy comes to the rescue for this puzzle.
I think the '6's are the easiest to look at.
There are two sets of interlinked pairs, The yellow/red set are in Be; Fa and Fe.
The green.blue set are in Aa; Ad (row A) to Dd (column d) to Db (row D) and finally
Bb (column b).
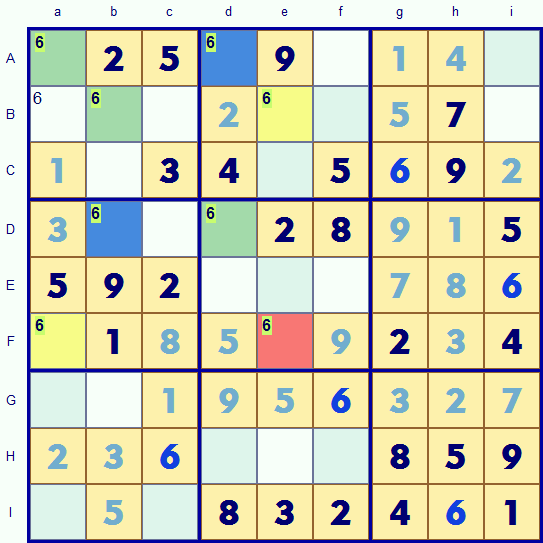
The yellow and red squares do not help much, the green and blue do though. Region Aa has two green squares. This is not allowed so the 6s can not go in the green squares so they MUST be allocated to the blue squares Db and Dd. This in turn forces Ba to be a 6 in region Aa and therefore also the red square Fe. With all the 6s allocated the rest are easy.
Any comments ? Click here to contributeAlexander, thanks very much for your easy to follow explanation. It has expanded my practical knowledge of alternate pair coloring.
Any comments ? Click here to contributeCopyright © 2005-2024 Sudoku Dragon