Sudoku Trial and Error

Call it what you will back-tracking, guessing, labyrinth or trial and error, Sudoku players are divided as to whether this is a proper solution technique.

The strategy is simplicity itself and can be used on its own to solve every Sudoku puzzle. You just choose one available possibility for a square, remember what you have chosen and then proceed to solve the remaining squares. If you made the wrong choice then the puzzle will become un-solvable (see separate page on how you can detect this). A Sudoku puzzle is not solvable when two squares in the same region have the same number (breaking the rules) or as a square in a region is unable to take any number at all (again breaking the rules). If this happens you have to back-track all the allocations until you come back to the last square you guessed, and then choose one of the other alternatives, you have knocked out one of the possible alternatives.

If you are solving with pencil and paper this technique often becomes a real mess of marks and rubbings out as choices are made and unmade. With the help of a program such as Sudoku Dragon this is not a problem as it lets you easily undo and redo previous square allocations, it also lets you put a note on a square to indicate where you made a ‘guess’.

For most puzzles the standard set of strategies enable you to make a definitive choice without needing to guess. Many players hate having to make an allocation on the off chance it is correct, they want to work it out entirely be logic as to what goes where for sure. But if you think about it then many of the strategy rules are actually all about looking ahead at the knock on effects of making an allocation. If when you are seeking to allocate a square and find yourself thinking on the lines of “if I put a 3 here I would have to put a 3 there and that is incorrect” you are doing a little thinking ahead and backtracking.

Another reason why you might choose to ‘guess’ is when a puzzle can be solved much faster than looking for the more esoteric solution strategies. By the time you have looked for X-wings, swordfish, hooks and alternate pairs you might just as well have tried solving a square by trial and error.

Ensuring that a puzzle can be solved only using the well known strategies, and not require a guess, is hard for puzzle generating software. If you look on the Internet you will find that most puzzle generators do use a lot of trial and error to work out if a puzzle is solvable, they do not follow the techniques that a human solver would use. Sudoku Dragon is different, it follows a set of strategies in increasing degrees of complexity until it reaches a solution.

To see how you can solve a whole Sudoku puzzle just using trial and error take a look at this external web site that has an animated example : Animated Sudoku solver ➚

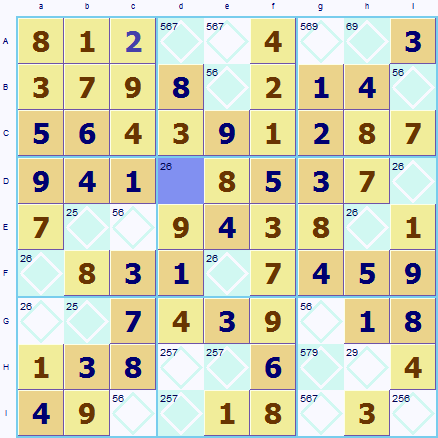Let's look at an example of how trial and error works. Here is a puzzle that has reached a seemingly impassable stage. Sudoku Dragon has highlighted all the possibilities on all the squares and there are no 'standard' rules (only choice, shared exclusion, excluded twin etc.) that yield a new square to be set.

With trial and error you choose a square with only two possibilities as then the chances are just 50:50 of the guess being correct. Look at the highlighted blue square Dd, it can take only a 2 or a 6. So let's try a 2. This immediately opens things up a lot, 6 must then go in Fe (only choice in region Dd) a 2 in He (only square in column e) and a 6 in Di (only choice in row D).

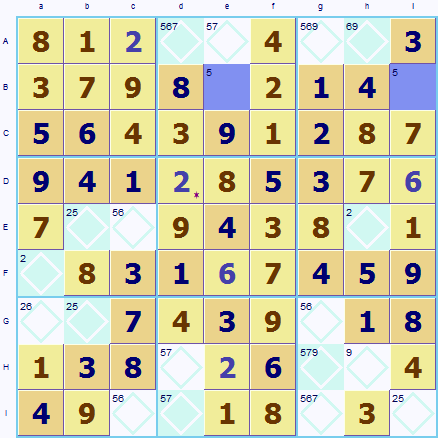
This brings the puzzle to a sad state of affairs. Our original square Dd is highlighted in green, and now a problem has arisen in squares Be and Bi (highlighted in blue). [Sudoku Dragon has been used to add an annotation to Dd marked by a * in the bottom right corner.] A 5 must go in Be because it is the single possibility left for this square. But Bi must also take a 5 as it is also the single possibility left for this square. As Be and Bi are on the same row this can't be true. You cannot have two 5s in the same row. So our original guess for Dd was wrong, it cannot take a 2 it must be the only other option a 6. Using Sudoku Dragon you can quickly backtrack and make the alternative assignment of 6.

Sometimes it will take many steps to prove one option was an incorrect guess and that can make it a slow and laborious process.

For a further in-depth guide  click here

Solving without guessing

So if you are to solve this same puzzle without guessing, how is it to be done? This is indeed a hard puzzle. If you look for a square to solve with the simpler strategies ‘only choice’, ‘single possibility’ and ‘only square’ nothing is evident. If you extend this to looking for ‘sub group exclusions’, ‘twins’, ‘triplets’ and ‘chains’ still no luck. This has all taken quite some time to do. Now we must look to more esoteric solution strategies. It turns out that an X-Wing is present, if you look at where 2s are possible you will spot a box in Row D and Row I, however this only knocks out a 2 occurring in Hd and does not allow a square to be solved. So what next? The last recourse is to the more advanced solution strategies. The key is to use the alternate pairs coloring of where 6s can occur. If you do this you will find that quite a few squares that looked as if they could take a 6 but can not. One such square is Be that can not be a 6, so it must be a 5 and the 6 in region Ad must go in Ae. Once this allocation has been made, all the remaining squares can be easily solved. So who said solving Sudoku puzzles is easy? Sometimes making a guess can save a lot of time.

Mazes

The trial and error technique is a general technique (or algorithm) for solving all sorts of problems. The most familiar example is finding your way through a maze. You can always escape from a maze as long as you run through all the alternative paths in a consistent, logical fashion. If turning right leads to a dead end or leads back to somewhere you have been before, retrace your steps and try straight ahead, if that fails try left. In this way all of the possible alternative routes are tried out in turn - until you find the path that lets you escape the maze.

Unless you are careful you can end up literally going round in circles. To stop this you need to record where you have been and what route you took. This can be done by unraveling a thread; if you come across the thread again later on, you have done a circuit and must try another route (no longer following the thread). More practical alternatives are a bag of rice or a stick of chalk, anything that can mark which options you have already tried. If you choose rice, put a grain at each junction to mark the turning that you took, if you find a grain ahead of you then you’ve repeated yourself and must try an alternative path.

Computers can use this technique to solve any maze problem with ‘brute force’. The algorithm just runs through each possibility in turn, e.g. ‘turn left at each junction until reach dead-end, then backtrack and then instead of turning left, turn right’.

The analogy with Sudoku is strong as ‘trial and error’ is using very much the same idea. When navigating through mazes an experienced human can make educated guesses on the most promising path rather than slavishly trying each option in turn. Similarly a skilled Sudoku player can dismiss unpromising options to reach the solution much quicker than just ‘guessing’.

The Labyrinth

In ancient Greek myth the Minotaur ➚ (a monstrous combination of bull and man) was devouring an annual tribute of the young people of Athens (seven maidens and seven youths). The hero Theseus ➚ determined to put an end to this cruel tradition. He volunteered to be part of the following year's tribute and when Ariadne ➚ (King Minos ➚'s daughter) saw Theseus, of course she fell in love. To help him kill the Minotaur she gave him a magical ball of thread devised by Daedalus ➚ (the famous inventor). The ball magically unraveled to show the route to the center of the Labyrinth and the Minotaur. [The Labyrinth was an especially fiendish type of maze devised by Daedalus himself]. Then, having slaughtered the monster he just needed to follow the thread back to escape the maze. Ariadne and Theseus soon grew tired of each other and went their separate ways.

Copyright © 2005-2024 Sudoku Dragon