Sudoku Puzzle

Sudoku is an intriguing puzzle of patterns and cryptic rules. Regular Sudoku consists of a square grid to be filled in with numbers 1 to 9. The puzzle is to place these symbols in the correct place to complete the grid. Sudokus have been developed in many forms, they do need not be number based and can be letters or colors or shapes or whatever you like; it is a very varied type of puzzle.

There is just one simple rule controlling where you can place numbers in the regular Sudoku puzzle. A symbol must occur once and only once in each group of nine grid squares. The groups of nine squares include the rows, columns and regions within the puzzle. Such a simple rule leads to all the amazing range of Sudoku puzzles.

Take a look at our pages on the history of Sudoku, Sudoku solution strategy and theory.

Sudoku Terminology

First let's introduce the terms used on this web site, as not everyone uses the same convention. The whole puzzle area is called the grid, it is divided into rows (horizontal lines) and columns (vertical lines) made up of individual Sudoku squares.

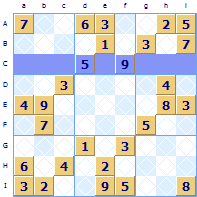
Rows

To save confusion we use letters rather than numbers to refer to rows and columns. The names are shown in the grid heading. In this Sudoku grid row C (capital C) is highlighted. Note: If we used numbers we would end up having to say things like in row 3 there is only one place for a 5 while in column 2 there are 3. Confusing isn't it? Using letters for grid references makes it easier to follow.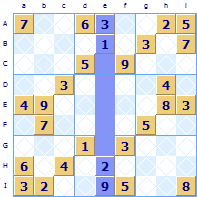

Columns

Sudoku columns are given a lower case letter.
Column e (small e) is highlighted.
Using row and column letters lets us unambiguously refer to squares. For example square He is row H column e, this Sudoku square has a 2 allocated in the example puzzle.

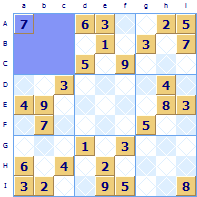
Regions

A region is a block of nine adjacent Sudoku squares, in the example puzzle the top left region Aa is highlighted. The whole grid is made up of nine regions. Some Sudoku sites use the term ‘mini-grid’; ‘box’ or ‘sub-grid’ for ‘region’. We think region is simpler and easier. A region is referenced by the top-left square, so region Dd is the central region. A symbol must occur once and once only in each of the regions within the grid as well as each row and column. This was one of the innovations that made Sudoku such an interesting puzzle to solve.

Groups

A ‘group’ is a general term for a group of nine squares in either a row, a column or a region.

Rules

How to solve Sudoku puzzles

The process of solving a Sudoku puzzle is to fill in the empty squares. Each puzzle has a single, 'correct' solution, each unallocated square has one correct value from the 9 possible values.

Sometimes it is fairly obvious what number must go in a square while other squares require a great deal of mental torture to solve. To work through all the possibilities it can take half an hour to solve one square! Much like placing a single piece in a jigsaw, there must be a place for a number to go but spotting the correct place may be easy or take an age to do.

There is no correct sequence of square allocations to make, different people use their own strategies to solve a Sudoku puzzle and so will solve the squares in a different sequence. However, the end result is always the same, there is only one unique solution, just many ways of getting there.

There are a number of standard techniques or strategies to help solve a Sudoku puzzle. We have guides built into our Sudoku solver demonstrating these strategies. We also have a Sudoku strategy page containing a description of all the commonly used methods: only choice, only square, single possibility, excluded hidden twins, naked twins, sub-groups and X-Wing. The more Advanced strategies are explained on a separate page: X-Y Wing and Alternate Pairs. There is a page on Sudoku theory too.

You can visit our online discussion forums. Sudoku Dragon comes complete with guides that take you through the most useful solution strategies step by step.

Making mistakes

If you make an incorrect allocation of a number in a Sudoku puzzle then the puzzle becomes 'unsolvable'. At some later stage you will find an insurmountable contradiction, a number would have to be placed in two squares in the same row, column or region violating the Sudoku rule or else you'll find a square that can't take any of the numbers according to the rule. To correct the mistake you need to backtrack through the allocations that you have made until you find the one in error. Often this is because you overlooked another possibility for a square and thought it was the only choice.

Creating Puzzles

Skill is required to create a challenging Sudoku puzzle. It is not just a matter of randomly allocating numbers to squares. Firstly, to ensure that there is only one unique solution requires that there is the correct number of initial 'exposed' squares to begin with. If there were only a handful there would be many ways to allocate all the squares - but all Sudoku puzzles can have only a single, unique solution. The challenge is to reveal just enough squares to make the solution both unique and challenging. The pattern of squares can make a pleasing arrangement , and this should be taken into account when creating a Sudoku puzzle. In general the more revealed squares there are the easier the puzzle will be to solve. If the revealed squares are distributed evenly throughout the puzzle, then it will be easier to solve than if regions have very few filled squares. Some of the toughest puzzles have a couple of regions with no squares revealed at all, or when a particular number does not occur in the whole Sudoku puzzle. Solution strategies are discussed in our online forums and strategy page.

When Sudoku was published by the Nikoli magazine in Japan they decided to add some extra spice to form true Sudoku puzzles. They decided to make the pattern of revealed squares symmetric. If you turn the Sudoku on its side or upside down the pattern of initial squares is repeated (but not the numbers). Sudoku Dragon supports both a symmetric and a random pattern of initial squares. The random pattern can make the games more challenging to solve although it may be less aesthetically appealing to look at.

Sudoku Puzzle Difficulty

A good Sudoku puzzle has to have just the right level of difficulty. This decision is tricky because there are many solution strategies and different people will naturally find puzzles more challenging than others. The vital measure in establishing the level of puzzle difficulty is working out which Sudoku strategies are needed to solve it. The easier puzzles require the basic only square; single possibility and only choice rules. Moderate puzzles require some application of the twin and excluded choice rules. Truly challenging puzzles require the discovery of X-Wings, X-Y Wings, alternate pairs or may be even some use of trial and error: backtracking after following a blind alley or two before the correct solution is attained.

Sudoku and Jigsaws

The closest puzzle to compare to Sudoku is perhaps the humble jigsaw. There are similarities both in the way it works and the pleasure gained by solving it. In a jigsaw there are lots of pieces to fit in to a rectangular pattern, there is only one solution and each piece can only go in one place. Sudoku is also a matter of putting things in the right place. If you like doing jigsaws you'll enjoy Sudoku too.

To solve a jigsaw everyone will put the pieces together in different orders. Most people will hunt and separate the edge pieces and then join these up before tackling pieces with distinct markings and then join these up. When nearing the completion of a jigsaw, particularly with problem areas such as large expanses of clear blue sky, you may look out for pieces of a particular shape. There are different strategies to apply depending on the stage of completeness and that makes jigsaws interesting.

Sudoku is just the same, there are strategies to use at the different stages of solving the puzzle. Some of these can become a tough trial and error process just like a jigsaw.

The joy of successfully completing a jigsaw is akin to that of solving a Sudoku puzzle, when the final square has been filled in, the satisfaction of correct completion is like stepping back to enjoy the whole picture when the final piece has been placed in a jigsaw. Everything is in its proper place.

Sudoku puzzle types

Starting from the standard Sudoku rule there are many ways to create a range of different types of puzzle. First of all you can change the size of the grid. Using the regular 9x9 grid is just one option. The simpler 4x4 grid is useful for learning the basics of Sudoku and we use it for some of our guides. With 4x4 there are only four symbols and four regions to consider, and so 4x4 can never make a hard puzzle.

Stepping up to larger sizes a grid of 16x16 makes a real challenge, because there are now 16 squares with 16 possibilities for each square. With this size there are not enough digits so the letters 'A' through 'I' or 'hexadecimal' digits will do admirably instead. Sudoku Dragon supports puzzles of this size. The sudoku grid size can be arbitrarily increased further to 25x25 and 36x36 and so on, but 16x16 with a total of 256 squares to complete is surely challenging enough; after that the puzzle has too many possibilities to carry around in the average sized mind.

You can also use rectangular regions to make up the grid rather than squares. Sudoku Dragon supports seven rectangular grids including: 2x3 grid (about the most common rectangular size you will find) and the 4x5 (or 20x20) monster sized grid. Here's an example of 2x5 rectangles making up a 10x10 puzzle.

Our Theme and Variations page describes the many different types of Sudoku available. These include Chinese numbers; Word Sudoku; X Sudoku and Super-Sudokus or Samurai Sudoku with their overlapping 3x3 puzzles that have five overlapping puzzles to solve in one large puzzle.

How many possible puzzles?

For information about the history of Sudoku, please see our History page. For help on solving Sudoku puzzles visit our Strategy page or our theory page.

See also
Background ➚ news story about the rise in popularity of the puzzle
Daily Sudoku ➚ Provides a daily puzzle but no solver.
The Guardian ➚ Daily sudokus of various types and an active online community.

Please share your interest on Facebook, Twitter, Pinterest, Tumblr or Mix using the buttons. Please visit our (secure) contact page to leave any comments you may have.

Copyright © 2005-2024 Sudoku Dragon