Theme and Variations
Many different forms of Sudoku have been invented. Some are straightforward extensions on the original idea of Sudoku while others are rather strange.
Grid Size
It turns out that the regular 9x9 puzzle is just the beginning. There are no limits on the size of the puzzle. You can make a puzzle smaller and simpler, or larger and harder to solve by changing the size of grid. Commonly used Sudoku sizes include 2x3 regions rather than the normal 3x3 so there are six numbers to place in the squares rather than nine and 4x4 where there are sixteen numbers. Our theory page gives more detail; there is no theoretical limit on how large the grid size can be. The same old strategies can be used to solve Sudokus of different sizes.
Puzzle size grid 6x6 made up of 2 by 3 blocks

Puzzle size grid 14x14 made up of 2 by 7 blocks
Puzzle size grid 20x20 made up of 4 by 5 blocks
Sudoku Dragon can generate and solve all these sizes of puzzle along with a great many more.
Colors, Words, Pictures and Symbols
Although Sudoku places numbers in the correct squares; it has nothing to do with arithmetic. The familiar numbers 1 to 9 can be replaced with anything at all, as long as each 'square value' is different from the other. A puzzle just needs a set of nine different things of any type: colors; letters or picture fragments. Sudoku Dragon supports a version using Chinese characters in place of numbers. If it uses picture fragments then one of regions (usually the central one) will show the completed picture, but you really need a program to help you play these picture Sudoku puzzles as you can't easily pencil in sketches of possibilities for the missing squares!


See Also: Picture Sudoku ➚ and Word Sudoku ➚
Wordoku or Word Sudoku
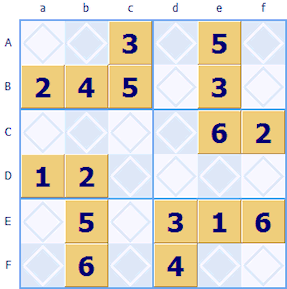
If letters are used in place of numbers then words can appear in the grid, often this is a hidden nine letter word in a row or column. Here's an example of a puzzle with its solution alongside, the hidden word POWDERING is in the center row.
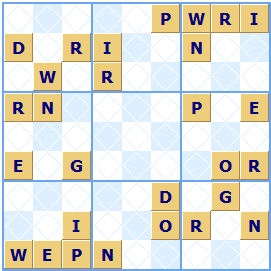

In this second Wordoku puzzle generated by Sudoku Dragon the hidden word is in the second row. The hidden word is Diplomats.
see it in Sudoku Dragon click here...
Sudoku Dragon fully supports Word Sudoku. The popular grid size 9x9 has a hidden nine letter word.
Chinese numbers
The Arabic numbers 1 to 9 do not need to be used for Sudoku, you can just as well use the Chinese numbers for 1 to 9 (一 to 九).
So while playing Sudoku you can also learn the numbers in Chinese ➚.
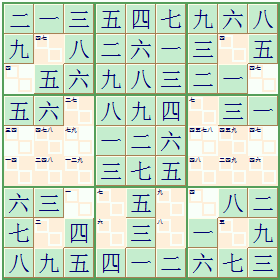
see it in Sudoku Dragon click here...
Chinese phrases
The word version of Sudoku can be in any language. All you need is a phrase with nine different characters.
Sudoku Dragon has chosen Chinese characters, so the puzzle hides a Chinese phrase. Sudoku can then become a convenient way of learning some Chinese characters ➚.

see it in Sudoku Dragon click here...
Abstract symbols
Going one more step beyond numbers, letters and Chinese you can also use abstract symbols in Sudoku Dragon.
We have used some of the astrological symbols ➚ for the zodiac as our symbols, but any old symbols will do.
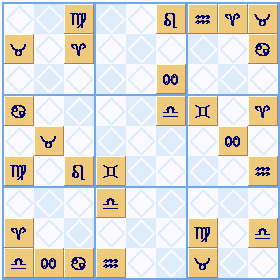
see it in Sudoku Dragon click here...
Jigsaw or Squiggle Sudoku
In regular Sudoku all the regions in the puzzle have an identical shape - a square or a rectangle. In Jigsaw Sudoku, the regions have different shapes, but each shape has to be contiguous and has the same number of squares as all the other regions. The strategies have to be changed a bit. The two-out-of-three strategy, which is so useful for regular puzzles, has to be overhauled and the shared subgroup exclusion rule needs to account for the individual pattern of overlaps in each Sudoku.
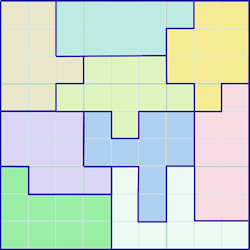

In this second example puzzle generated by Sudoku Dragon the irregular regions have different colored backgrounds. The pattern of regions is symmetric (180%deg; rotational).
see it in Sudoku Dragon click here...
Sudoku Dragon fully supports Jigsaw Sudoku for grid sizes up to 10x10.
See Also: Jigsaw Sudoku ➚
Neighbor Order
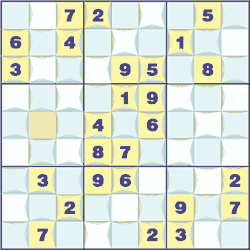
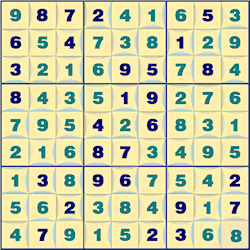
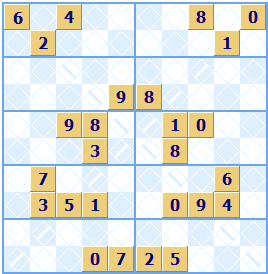
Displaying the numeric order of neighboring squares is a neat idea of adding extra information to help solve the puzzle. The border between two squares is used to give a hint as to which neighbor is larger than the other. It has a pointer towards the smaller of the two numbers. It is also known as ‘Greater than Sudoku’. For example a row containingf 9; 8 ;7; 2; 4; 1; 6; 5; 3 has the ordering 9 > 8 > 7 > 2 < 4 > 1 < 6 > 5 > 3. This extra information gives a new solution technique. If you a square has a 2 and its neighbor is smaller value then it must be a 1, similarly an 8 with a higher square neighbor must be a 9.
Here is an example puzzle with all the orderings shown in each square's border. In this case the square Bb can be immediately solved as it has neighbors 6 > x > 4 and so x must be 5.
To make solution a little harder only some of the neighbor borders may show the order. Often the initial grid is empty except for the neighbor ordering. A puzzle number ordering added is not strictly ‘Sudoku’ any more, as a picture or color Sudoku puzzle doesn't have a concept of order of neighbors. To a purist it is not quite the same thing.
See Also: Greater-Than Sudoku ➚
Thermo Sudoku
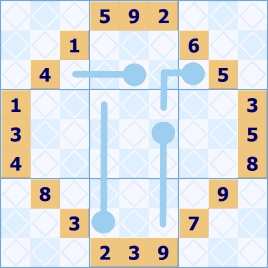
A site visitor kindly drew our attention to a variant of ‘neighbor order’ which is somewhat more appealing. It is called thermometer Sudoku because the grid has a number of thermometers among the unallocated squares. The squares along the thermometer must be allocated in sorted order along the thermometer so a three square sequence starting at the bulb could be 1;5;7 or 1;2;3 or 6;7;8. The thermometers can turn corners and be of any length from 2 to 9.
Stripe
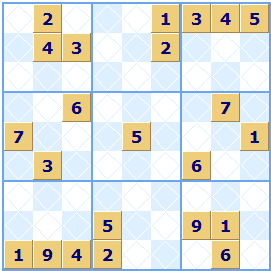
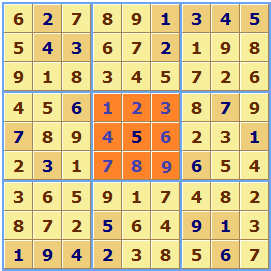
We at Sudoku Dragon have added our own little extension to Sudoku. Optionally one group in the grid will contain the numbers in ascending order (1 to 9) or descending order (9 to 1). The stripe may also be wrapped up into a region which can make it hard to spot. We have a whole page devoted to describing the stripe. In this example the stripe was hidden in the central region.
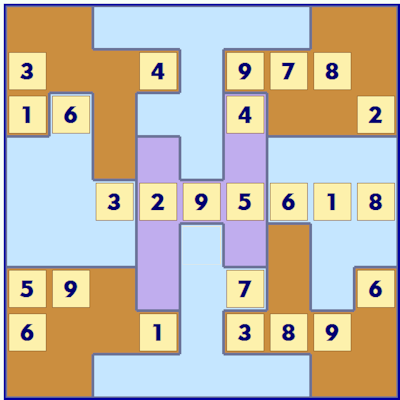
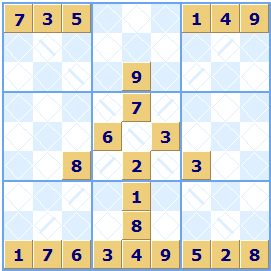
X Sudoku
If you go back to Euler and the origins of Sudoku with Magic Numbers and Latin Squares, his puzzles had rules about the diagonals as well as the rows and columns. X-Sudoku or Diagonal Sudoku has the numbers 1 to 9 occurring once in both diagonals as well as the rows and columns. You can make use of this extra rule to solve squares.
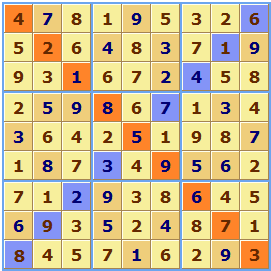
In this second example puzzle generated by Sudoku Dragon a grid size of 2x5 is used (ten squares per group).
The diagonal type of the Sudoku puzzle is indicated by the diagonal marks in the unallocated squares.
see it in Sudoku Dragon click here...
Sudoku Dragon supports X-Sudoku. All the many grid sizes can have the diagonals as an extra group.
See Also: Sudoku X ➚
Samurai Sudoku
Most players find keeping track of the nine numbers in a 3x3 grid an adequate challenge but others like a bigger puzzle.
The Samurai Sudoku provides this. It adds a new feature to Sudoku puzzles - overlapping puzzles. One or more regions within a puzzle are shared with another puzzle of the same size. The regular grid size for puzzles of this type is the 21x21 square grid that contains five regular overlapping 9x9 puzzles. We have a whole page on Samurai Sudoku explaining the special techniques you need to solve them.
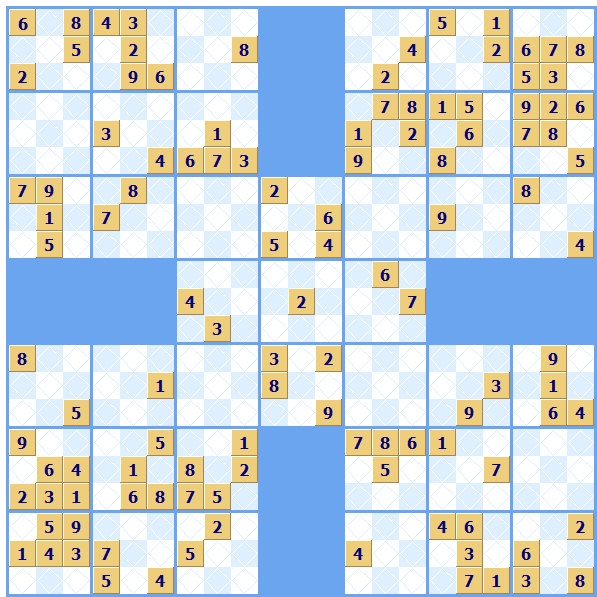
Sudoku Dragon supports the Samurai variation of Sudoku at puzzle sizes 21x21 and 8x8.
see it in Sudoku Dragon click here...
Killer Sudoku
Another way to extend Sudoku is to add some mathematics on top of the normal Sudoku rules. In Killer Sudoku ➚, the standard grid is divided up into collections, in the top left square of the collection is the sum of the numbers that go in the squares making up the group (row or column segment). It is also known as ‘Sum Sudoku’ and ‘Sumdoku’. This lets you solve squares in new ways, in the simplest case you could have a collection of only two squares, if the sum is 3 then you know one square in 1 and the other 2, or if the sum was 17 then they must be 8 and 9. So the sum is giving extra information about the numbers in the squares quite apart from the standard ‘number unique to a group’ coming from Sudoku. A key starting point is to look for collections with a low average (e.g. a total of 6 for 3 squares, average 2, means can only be {1, 2, 3}) or a high average (e.g. a total of 30 for 4 squares, average 7.5 means can only be {6,7,8,9}). Usually the extra information is sufficient to start off with an empty grid and yet still be able to be solved.
There are further variations on this theme when not just addition is used but subtraction, multiplication and division too - there variants are called ‘Mathdoku ➚’; ‘KenKen’; ‘Kendoku and ‘Calcudoku’.
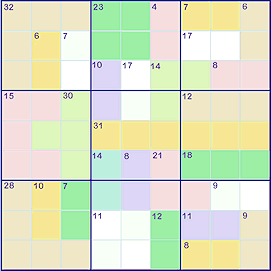
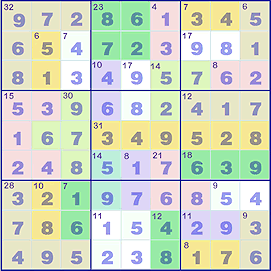
See Also: Killer Sudoku ➚
Other Variations
There are a host of other variations on the basic theme and new ones are being invented all the time. If you have found one that you like let us know about it.

Any comments on this page? Click here to contribute.
Copyright © 2005-2025 Sudoku Dragon
