Samurai Sudoku

Many newspapers set a Samurai Sudoku as a weekend challenge. We offer a free daily Samurai puzzle every day, and you can generate and solve them with our Sudoku Puzzle Generator.

They look formidable as they are made up of 5 overlapping standard Sudoku puzzles with a grid containing a total of 369 squares.

Apart from the sheer number of squares to solve, Samurai Sudokus are not really harder to solve than the regular 9x9 version.

Now look at a puzzle in more detail and all those hundreds of squares. We have color coded the five regular 9x9 Sudokus that make it up.

We are going to look at the overlapped regions in more detail later and so have highlighted one area with a yellow rectangle.

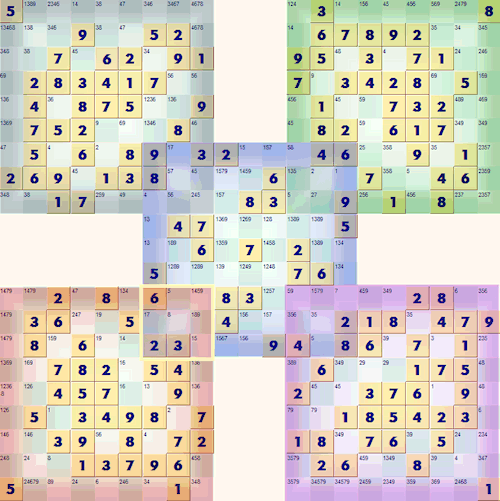
All the squares that do not overlap can be solved using the standard solution strategies you use for regular 9x9 puzzles. Of the total of 369 squares there are only 4 sets of 9 squares (36) that are shared between two puzzles. All the remaining 333 squares in the grid belong to only one puzzle.

This particular Samurai puzzle has 204 squares remaining to be solved. What about the overlapping squares? Each square in the four overlapping regions is in five groups of squares rather than three in the ordinary case. They belong to two rows; two columns and one region. This makes these squares easier to solve as generally more possibilities are knocked out, this is the only real twist you need to learn when solving these puzzle. Looking at the example puzzle in more detail, consider the lower left puzzle (highlighted in red) on its own.

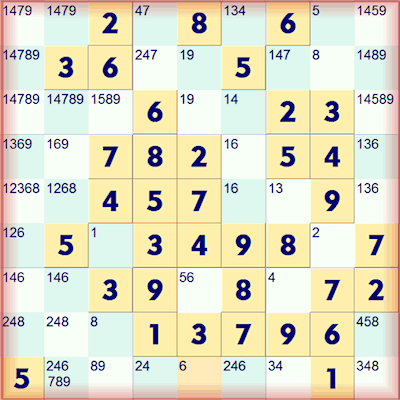
This 9x9 part of the Samurai is not a solvable puzzle. There is more than one solution to it. If you solve all the squares you end up with this situation with no more squares that can be solved.

Similarly look at the central puzzle (highlighted in blue) on its own.

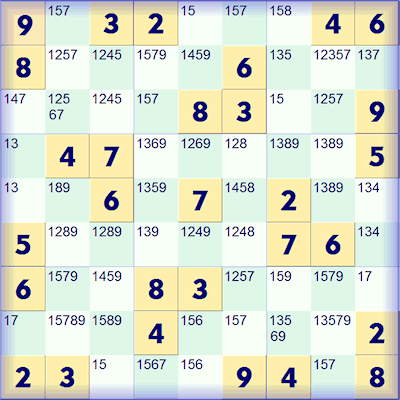
Once again, this is a bad puzzle, it cannot be solved. After solving as many squares as possible you end up with the following sad state of affairs.

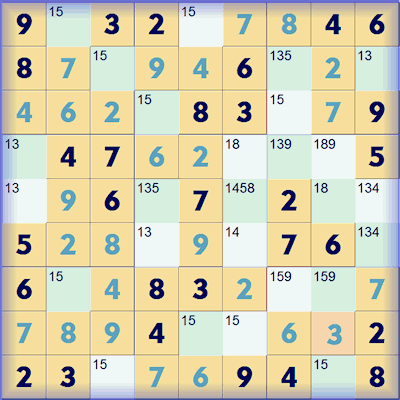
However the full Samurai Sudoku puzzle can be solved as a whole when the puzzles are combined because of the squares in the overlapping regions. Now we will concentrate just on the overlapping region highlighted in the Samurai with the yellow rectangle between the 'red' and 'blue' puzzles. Let's look at the possibilities from the two puzzles in isolation. The first extract shows the region as the top right region of the bottom left (red) puzzle with all the possibilities marked. The second shows the same squares as the bottom left region of the central (blue) puzzle with all the possibilities marked.

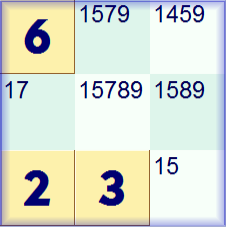
As the squares are shared in the Samurai the possibilities marked in one sub-puzzle must also be possible in the other. So the actual possibilities are only those common to both. To put this altogether, the shared squares have the possibilities shown. The possibilities with a red background are not possible because of the intersection with the lower left red puzzle. The possibilities with a blue background are not possible because of the intersection with the center blue puzzle.

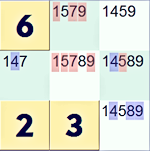
So that is a combined 15 possibilities that can be dismissed because of the overlap of the two blocks of 9x9. Using these restrictions on possibilities the whole Samurai puzzle can be solved.

Sudoku Dragon helps you solve Samurai puzzles by explaining which possibilities are and are not possible. Because of the large grid size it has to use a different way to refer to squares, it uses P1 to P5 to identify the 5 puzzles within a Samurai. So in Sudoku Dragon's explanation as to why square Nh can not take a 2 it explains the existing occurrence of a '2' in both puzzles bottom left and central sub-puzzles.

Impossible because Region 'Mg P3' already contains '2' and because Row 'N P5' already contains '2'.

Any comments on this page? Click here to contribute.

Copyright © 2005-2024 Sudoku Dragon